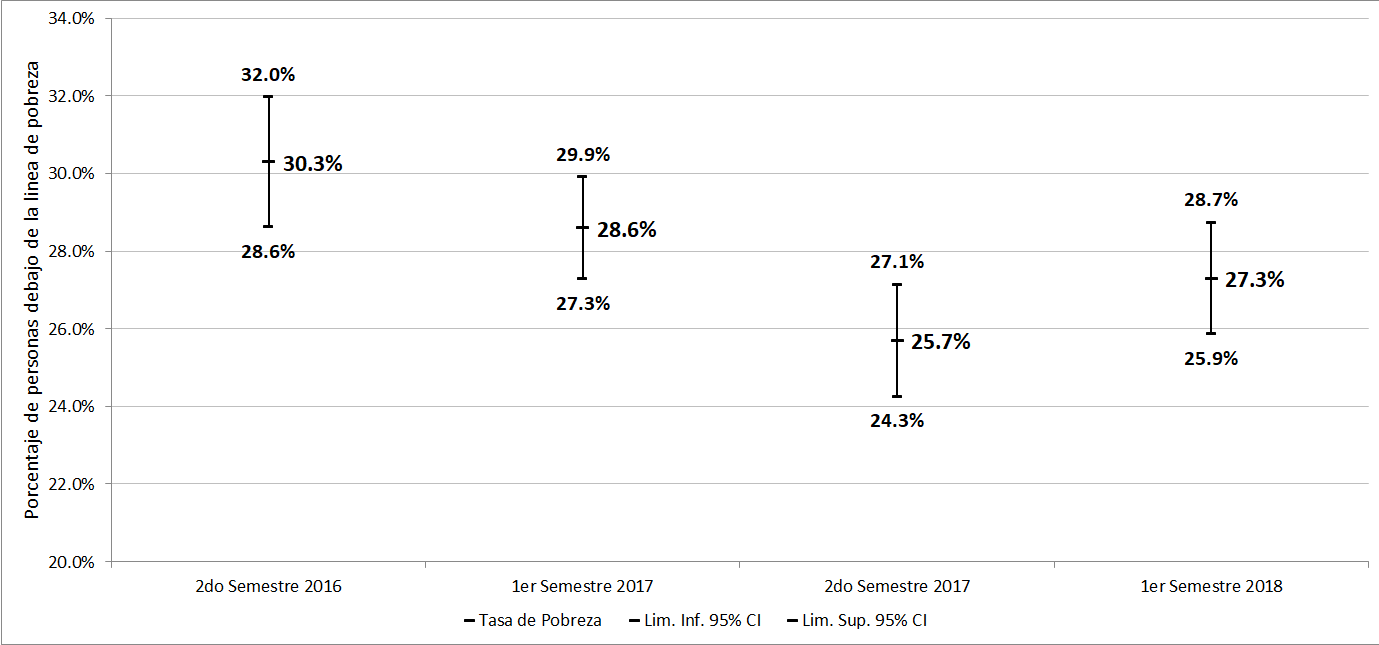
Hace un par de semanas el Instituto Nacional de Estadística y Censos (INDEC) publicó la estimación de la incidencia de la pobreza urbana para del primer semestre de 2018. La medición dio 27.3% y la interpretación usual es que este es el porcentaje de personas debajo de la línea de pobreza en la población urbana.
La Encuesta Permanente de Hogares (EPH) releva una muestra de hogares representativa de 31 aglomerados urbanos, por lo que para conocer el verdadero valor de la tasa de pobreza en la población urbana hay que considerar la variabilidad de la estimación. Esto es, si se seleccionara otra muestra representativa de los 31 aglomerados urbanos la estimación de la tasa de pobreza ¿sería la misma? Probablemente la nueva estimación estaría cerca de 27.3% pero es muy difícil que de exactamente el mismo número. Es decir, hay cierta variabilidad en la estimación asociada a la selección aleatoria de las viviendas que componen la muestra. Existen varias formas de medir esta variabilidad. Una forma de medirla es a través de la construcción de intervalos de confianza. Con los datos publicados por el INDEC, el intervalo del 95% de confianza, por ejemplo, va desde 25.9% hasta 28.7% (ver Figura 1). La interpretación estadística de este intervalo es que si uno pudiera seleccionar aleatoriamente muchas muestras (muchas EPH) de la población urbana en el primer semestre de 2018 y repitiera la estimación de la pobreza y la construcción del intervalo del 95% de confianza, 95% de esos intervalos contendría al verdadero valor del parámetro poblacional (en este caso la tasa de pobreza en la población urbana en el primer semestre de 2018). Una interpretación habitual del intervalo de 95% de confianza es que es un intervalo que con el 95% de probabilidad contiene al verdadero valor de la incidencia de la pobreza urbana en el primer semestre de 2018. En otras palabras, con 95% de probabilidad la incidencia de la pobreza en la población urbana está entre 25.9% y 28.7%. La mitad del ancho del intervalo de confianza se conoce como margen de error y todo este procedimiento se conoce como inferencia estadística. La inferencia estadística nos permite afirmar, con cierta probabilidad, cual es el verdadero valor de la tasa de pobreza en la población urbana en el primer semestre de 2018.
Figura 1. Estimación de la Incidencia de la Pobreza Urbana
Nota: elaboración propia a partir de los datos oficiales publicados por INDEC.
A modo de ejemplo, antes de cada elección presidencial, diferentes consultoras toman muestras del padrón electoral y calculan el porcentaje de votos que sacaría cada partido el día de la elección. Aun cuando las muestras representan a la misma población (padrón electoral) los resultados en cada muestra no son exactamente iguales, tienen variabilidad. Supongamos una de estas muestras representativas del padrón electoral. Sobre esta encuesta se podría estimar el porcentaje de votos que saca el partido X, 40% digamos. A nadie se le ocurriría, por ejemplo, declarar un ganador a partir de los resultados de una muestra sin realizar la elección (que revela el verdadero porcentaje de votos que saca el partido X en el total del padrón electoral). Las encuestas electorales, como solo son una muestra de la población bajo análisis, tienen un margen de error. Este margen de error, digamos 3%, establece que el partido X podría sacar entre 37% y 43% de los votos el día de la elección. El margen de error representa la variabilidad que tiene el porcentaje de votos estimado para el partido X a partir de esa encuesta. Por otra parte, en la comparación con el porcentaje de votos de otro partido, W, también se toma en cuenta este margen de error. Supongamos que el porcentaje de votos que saca el partido W en la muestra es de 36%, entonces podría sacar entre 33 y 39% el día de la elección. Esta situación se describe usualmente en los medios periodísticos como de “empate técnico», con estos resultados muestrales no podemos decir quién ganará entre X y W.
Con la EPH pasa lo mismo. En el caso de la pobreza, el “40% de los votos» corresponde al 27.3% estimado para la incidencia y el margen de error es de 1.4%. La incidencia de la pobreza “sacaría» entre 25.9% y 28.7% “de los votos el día de la elección» con un 95% de probabilidad. Sin embargo, es muy común que tengamos en consideración el margen de error en la interpretación del resultado de una encuesta política pero no en la interpretación de los resultados de la Encuesta Permanente de Hogares. En esta última, la interpretación de los resultados se hace como si las estimaciones se hicieran “el día de la elección y con todo el padrón electoral». Se interpreta la estimación de la tasa de pobreza del primer semestre de 2018 de 27.3% como si fuera el “verdadero» valor de la incidencia en la población urbana del primer semestre de 2018 sin considerar el margen de error de la encuesta. Es decir, hay un 95% de probabilidad de que la incidencia de la pobreza en la población urbana sea 25.9% o 28.7% o cualquier valor entre esos límites.
El mismo razonamiento se aplica cuando se quieren comparar dos estimaciones de la incidencia de la pobreza en el tiempo. Por ejemplo, para poder comparar la tasa de pobreza estimada para el segundo semestre de 2017 y la estimada para el primer semestre de 2018 hay que tomar en cuenta las variabilidades de las dos estimaciones (el margen de error de las dos estimaciones). En este caso, la inferencia se puede hacer mediante un contraste de hipótesis que establezca como hipótesis a contrastar que la incidencia de la pobreza en el total de la población urbana en el segundo semestre de 2017 es igual a la incidencia de la pobreza en el total de la población urbana del primer semestre de 2018. Denominando Π2sem17 a la tasa de pobreza urbana en la población del segundo semestre de 2017 y Π1sem18 a la misma tasa pero en el primer semestre de 2018, la hipótesis a contrastar es que Π2sem17 = Π1sem18, ó Π1sem18 – Π2sem17=0. Si se aceptara esta hipótesis se podría afirmar, con cierta probabilidad, que la incidencia de la pobreza no ha aumentado entre esos dos semestres.
Para contrastar la hipótesis se utiliza un estadístico de contraste y su distribución muestral. En este caso el estadístico de contraste está basado en las dos tasas de pobreza estimadas. Intuitivamente si la resta de p1sem18=27.3% y p2sem17=25.7% da un valor cercano a 0 entonces se podría afirmar que la tasa de pobreza no ha aumentado. Formalmente, este contraste se hace con el siguiente estadístico:
donde stderr(p1sem18 – p2sem17) es el error estándar de la resta de los estimadores. Este estadístico, en muestras grandes como la de la EPH, tiene distribución normal estándar. Para resolver el contraste se calcula el valor de t* y se lo compara con el valor crítico de la normal estándar para algún nivel de significación. Por ejemplo, si uno utiliza como hipótesis alternativa a la que se contrasta la afirmación de que la tasa de pobreza en la población urbana en el primer semestre de 2018 es mayor a la del segundo semestre de 2017 (Π1sem18 – Π2sem17>0) el valor crítico relevante de la distribución normal para un nivel de significación del 5% es de 1.64. En este caso si t*<1.64 se acepta la hipótesis de que la incidencia de la pobreza urbana es igual en el primer semestre de 2018 que en el segundo de 2017 (al 5% de significación), mientras que si t*>1.64 se puede afirmar con un 95% de probabilidad, que la tasa de pobreza ha aumentado. Si uno hace los cálculos a partir de los datos publicados por INDEC para esos dos semestres obtiene un t*=1.55. Este valor es menor a 1.64 y entonces se puede afirmar, con un 95% de probabilidad, que la incidencia de la pobreza en la población urbana se ha mantenido constante entre el segundo semestre de 2017 y el primero de 2018.
El mismo contraste se puede hacer si uno quiere saber si la tasa de pobreza urbana en el primer semestre de 2018 ha caído en relación a la tasa de pobreza del primer semestre de 2017. En este caso el valor de t* es de -1.31 y la comparación con -1.64 nuevamente sugiere que al 5% de significación la incidencia de la pobreza en la población urbana no ha caído entre el primer semestre de 2017 y el primer semestre de 2018.
Cuando se utiliza el margen de error de las encuestas, la evidencia empírica presentada aquí sugiere que la incidencia de la pobreza urbana en el primer semestre de 2018 no ha aumentado con respecto a la del segundo semestre de 2017 ni ha caído en relación al primer semestre de 2017 (“empate técnico»).
Estos resultados resaltan la importancia de utilizar el margen de error de las encuestas cuando se interpretan los resultados de la medición de la pobreza en un semestre dado y en la comparación entre diferentes semestres. Si el margen de error se utiliza habitualmente en el análisis de encuestas electorales sería deseable que se comenzara a usar también para interpretar los resultados obtenidos con las encuestas a hogares.