Encuestas electorales: Alchemy or Science?

Una semana antes del ballotage en la Ciudad de Buenos Aires que ganó Horacio Rodríguez Larreta, las encuestas estaban en todas partes, y los encuestadores aparecían por todos lados pronosticando, analizando e interpretando la situación política a partir de la lectura de sus trabajos de campo. Ello cambió en un santiamén. Las encuestas cayeron en desgracia y se sospecha no solo que no sirven, sino que se manipulan para distorsionar el proceso electoral. Este repentino cambio social no es nuevo en Argentina lamentablemente. No intentaré explicarlo pues no poseo justificación alguna para esta conducta social que, como mínimo, es descomedida. En cambio, trataré de explicar cuál es el alcance de una encuesta, qué tipos de errores pueden cometerse al realizarlas, y por último, mostraré que las encuestas de este último ballotage, no merecen estar bajo sospecha. No solo ello, diré también que es posible encontrar encuestas bien hechas en Argentina.

Inferencia a partir de muestras estadísticas

Inferir significa sacar conclusiones. La inferencia estadística nos proporciona métodos para sacar conclusiones a partir de datos. Lo nuevo de la inferencia es que utilizamos la teoría de la probabilidad para expresar nuestra confianza en las estimaciones que realizamos. La inferencia estadística es el proceso mediante el cual adquirimos información sobre una población a partir de una muestra. Cuando utilizamos la inferencia estadística, estamos procediendo como si los datos proviniesen de una muestra aleatoria o de un experimento aleatorizado. Si esto no es cierto, nuestras conclusiones pueden estar expuestas a cualquier tipo de objeción.

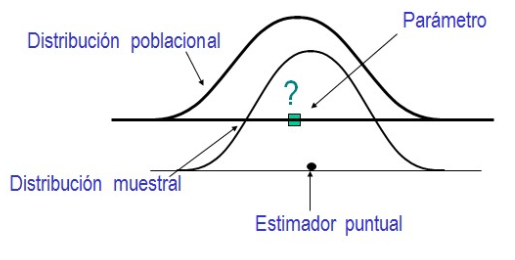
Consideremos una población sobre la cual deseamos estimar un parámetro, por ejemplo, la proporción que votará al PRO, sobre la base de una muestra estadística. Hay dos tipos de estimadores: a) estimadores puntuales y b) estimadores de intervalos. El estimador puntual infiere sobre la población estimando el valor de un parámetro desconocido en forma puntual, esto es, dándonos un único valor como estimación de dicho parámetro de interés. Ilustramos esto en la Figura I.

Figura I

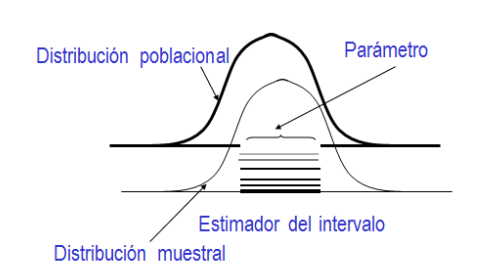
Un intervalo provee un conjunto de valores posibles sobre un parámetro poblacional desconocido. Un intervalo de confianza consta de dos componentes: a) un intervalo calculado a partir de los datos y b) un nivel de confianza asociado al mismo, el cual típicamente se fija en 95%. Ilustramos esto en la Figura II.

Figura II

Así, por ejemplo, utilizando una muestra estadística, podríamos decir que la intención de voto al PRO es de 55 puntos porcentuales, con un intervalo de confianza de ± 3 puntos porcentuales, lo cual significa que utilizando nuestra muestra, con una determinada confianza, la verdadera intención de voto al PRO se ubicaría entre 52 y 58 puntos. Denominemos a estos 3 puntos el error de estimación muestral (el cual, en la jerga de las encuestas electorales, suele llamarse margen de error. Puede ser menor a 3 puntos y los medios de comunicación deben reportarlo para cada proyección). Existe un trade-off entre el nivel de confianza y el error de estimación. Para los mismos datos, un error de estimación menor requiere que aceptemos un nivel de confianza menor. Asimismo, es más fácil estimar un parámetro con precisión cuanto menor es la varianza de los datos poblacionales. Debido a esto último, un incremento del tamaño de la muestra reduce el error de estimación para un nivel de confianza determinado. Entonces, si queremos reducir el error de estimación, debemos tomar muestras más grandes. En el límite, si tomamos como muestra a toda la población, no tendremos error de estimación alguno.

Error total de una encuesta

Dificultades prácticas, tales como la no-respuesta o la falta de cobertura de una encuesta, pueden causar errores adicionales que podrían ser mayores que el error proveniente del muestreo aleatorio. Una encuesta producirá mejores resultados si logra evitar los cuatro tipos de errores presentados en la Figura III.

Figura III

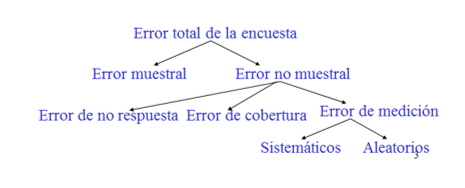
Como ya vimos, el error de muestreo se puede controlar aumentando el tamaño de la muestra. Mientras que los errores no muestrales (de diseño) no pueden reducirse aumentando el tamaño muestral. Así, por ejemplo, si un grupo de votantes de izquierda dice que  votará en blanco, pero en realidad no lo hace y vota a algún otro partido, este error de medición sistemático sesgará la estimación realizada a partir de la muestra estadística.

Finalmente, también hay que saber que entre el momento que se hace una encuesta y el día de la votación, generalmente, pasa un tiempo, quizás hasta una semana. En esa semana, no solo los indecisos terminan decidiendo su voto, sino que también, cambios en la opinión pública pueden alterar el voto de muchos otros ciudadanos.

Ballotage

Una semana antes del ballotage en CABA, la consultora Poliarquía, para el diario La Nación, proyectaba que Rodríguez Larreta obtendría 55,3% de los votos, contra 44,7% que irían para Lousteau. Estos resultados, y otros similares, fueron luego fuertemente criticados. Sin embargo, si uno los analiza cuidadosamente, no fueron tan errados. Rodríguez Larreta obtuvo finalmente 3.7 puntos menos que los arrojados por esa proyección, apenas un poco por arriba de un margen de error de 3 puntos. Por ejemplo, la misma consultora, también para el diario La Nación, pronosticó que en el ballotage de 2007, en CABA, Macri obtendría el 57.1% de los votos, contra un 42.9% que irían para Filmus. Los resultados finales fueron 60.9% contra 39.1%.

Me parece claro que el principal problema en el último ballotage fue que se puso todo el énfasis en la diferencia entre los candidatos, pues ello importaba para las PASO mientras que en el pasado, ello importó menos. Lamentablemente, y especialmente en un ballotage, donde los errores muestrales entre ambos candidatos están fuertemente correlacionados, medir la diferencia de votos con la misma precisión que el nivel de votos de cada candidato requiere muestras más grandes. Sin embargo, no creo que esto sea todo lo que ocurrió, pues es raro que la gran mayoría de las proyecciones de la diferencia de votos entre ambos candidatos estuviese sobrestimada si solo se tratase de un error muestral. También hubo un error de medición. Se esperaba que 8% del electorado votase en blanco y solo lo hizo el 5%, por lo cual 3% de los electores votó a uno de los candidatos –seguramente a Lousteau. Asimismo, hubo también error de predicción por no respuesta. Se argumenta que se podría haber proyectado mejor el voto de los votantes indecisos, pero ello requiere un modelo de comportamiento, algo que excede el trabajo de una encuesta. Finalmente, pudo haber cierto error de “cobertura” por las vacaciones de invierno.

Nada de esto justifica la descalificación generalizada de las encuestas ni de las firmas que las realizan. A modo de ejemplo, Poliarquía, en su página web publicó un documento en el que resume 10 años de pronósticos realizados para el diario La Nación. En 17 elecciones, siempre predijo correctamente el ganador de la elección y el que ocupaba el segundo lugar. Además, el margen de error promedio de sus proyecciones fue 1.4 puntos porcentuales.

Conclusión

Seguramente, como en todas las áreas, entre las firmas encuestadoras hay alquimistas, científicas, y deshonestas. Sin embargo, los resultados del último ballotage solo justifican interpretar más cuidadosamente los resultados de las proyecciones, saber que el margen de error puede ser grande y que hay otras fuentes de error de diseño que muchas veces no pueden evitarse. Las encuestas bien hechas, aun con sus errores, son un instrumento muy útil en la toma de decisiones de los ciudadanos. Por supuesto, me parece una muy buena idea que se informe quien financió cada encuesta cuando estas se dan a conocer.