Una pregunta clásica en economía (y administración) es ¿cómo diseñar esquemas de incentivos para equipos que sean óptimos desde el punto de vista de quien los diseña? En particular, ¿conviene usar premios a todo el grupo (joint performance evaluation) o premios a aquellos individuos que se hayan destacado más (relative performance evaluation)?
Para ser concretos, imaginemos que cada individuo de un grupo debe tomar acciones; llamaremos ai a las acciones del miembro i. Esas acciones no son observables para el “principal” (que diseña el contrato), pero determinan la distribución de probabilidades que seguirá un resultado observable, llamémosle y, que puede ser ingreso, pero puede ser también algo más general como y=(ventas, costos, satisfacción de clientes, etc.). Por ejemplo, si los agentes se esfuerzan mucho (digamos que eligen niveles de esfuerzo ai altos) es más probable que el nivel de producto y sea alto (pero no es una certeza).
Fijemos un perfil de estrategias (a1, a2,…, an), una para cada uno de los n individuos, que se quiera implementar (no siempre se quiere implementar “mucho esfuerzo” pues quizás sea muy caro para el principal si los empleados son unos haraganes, o si el nivel de producto no responde mucho al esfuerzo). Dado ese perfil, el principal se pregunta “¿cuál es el mejor contrato, desde mi punto de vista, para implementar ese perfil de acciones?”. Eso es, debe elegir cuánto pagarle a cada agente i, el salario wi, como función de qué nivel de producto y se observa. Después, se fija cuánto ganaría con ese contrato, y repite el ejercicio para todos los perfiles posibles de acciones. Cuando termina, elige cuál es el perfil que le da mayor utilidad o beneficio.
Un resultado clásico es que lo que se le paga al agente i es una función de cuánto nos “confirma” el nivel de producto y que el agente i hizo ai y no alguna acción alternativa bi. Por ejemplo, si en una tienda en Punta del Este unas ventas espectaculares sólo dependen de si la temporada es excepcional o no, no tendrá sentido pagarle mucho a los vendedores si las ventas resultan excepcionales, ya que pagar mucho en ese caso no ayuda nada para inducir un esfuerzo alto.
Aunque esa teoría ha rendido frutos increíblemente útiles, a menudo los resultados que arroja no parecen muy realistas. Una crítica típica, y razonable, es que los contratos óptimos según la teoría suelen ser infinitamente más complicados que los que observamos en la realidad. En la práctica, para incentivos en equipos, los esquemas de incentivos a menudo son lineales y no dependen del desempeño individual (a priori se establece que Juan se lleva 15% del bono para el equipo, Inés el 20%, etc.).
Estuve en la conferencia de la Sociedad Econometrica en Guayaquil el 9 y 10 de noviembre en una charla espectacular de Juuso Toikka, basada en “Robust Incentives for Teams” (con Tianjiao Dai) en que discutió un contexto en el cual los contratos óptimos son precisamente lineales, y no dependen del esfuerzo individual. Hoy quiero comentar el mecanismo, porque me pareció muy inteligente.
La intuición de por qué puede ser óptimo pagar a cada individuo sólo en función de los resultados del equipo es bien sencilla, y se basa en que naturalmente no es bueno darle pagos a cada miembro (que no estén completamente atados a los resultados del equipo). Con pagos individuales los agentes tendrán incentivos a maximizar sus pagos, y no los del equipo, y eso puede llevar a acciones malas en su conjunto (no colaborar, sabotaje, etc.). Si los pagos de cada agente dependen sólo del resultado del equipo, esos incentivos desaparecen.
Para ilustrar esa intuición, veamos cómo destruye un esquema que a priori parece razonable. Supongamos que el principal observa la producción individual de cada uno de sus dos empleados, y que ofrece un bono de $ b a quien produzca más, o $ b/2 a cada uno en caso de empate ($0 para el que produjo menos). Si el principal es un poco paranoico, y no sabe qué acciones tienen disponibles sus empleados, podría imaginar que cada uno tiene a su disposición la acción “sabotear al otro”, y que los pagos de ambos agentes si el individuo 1 sabotea son:
- Si 2 no sabotea también, $ b para el individuo 1; –c, menos el costo de la acción que tomaba 2, para el individuo 2.
- Si 2 sabotea también, $ b/2 para cada uno.
En este caso, sabotear es dominante: sin importar lo que haga el otro, a mi me conviene sabotear. Si el otro no está saboteando, gano lo máximo posible, $b; si el otro está saboteando, mi pago mejora de –c a $ b/2 si saboteo. El principal perderá $b, porque ambos se dedicarán a sabotear, y no a producir.
El principal se da cuenta que en este contexto el esquema de bono tipo “torneo” entre los empleados, no será óptimo. ¿Qué determina que no sea óptimo? Hay dos elementos clave: los intereses de los empleados no están alineados, y el principal considera posible que exista la acción de sabotaje (es un poco paranoico).
Desde hace unos años esta versión de paranoia se ha vuelto común en economía. Al menos desde el trabajo de Gilboa y Schmeidler (J. Math. Econ 1989) sobre aversión a la incertidumbre se modela a un individuo que desconoce exactamente en qué mundo vive (y que es averso a esa incertidumbre) como uno que elige acciones asumiendo que una vez que elija su acción, la naturaleza elegirá la distribución de probabilidades sobre estados que sea más desfavorable para él.
En este caso, Toikka y Dai asumen que el principal (el que diseña el contrato de incentivos para el equipo) desconoce qué acciones tienen disponibles los individuos, y asume lo peor. Asume que una vez que elija el contrato (el esquema de sueldos para los empleados como función de y), si hay algún conjunto de acciones para cada individuo que haría que él recibiera “lo peor”, ese es el mundo que elegirá la naturaleza.
Es un supuesto un poco extremo, pero sirve para pensar qué tan robustos son los contratos a la posibilidad de existencia de acciones que no estaban en el radar del principal. Más aún, esto es razonable cuando una institución grande diseña esquemas de incentivos que se aplicarán en distintas divisiones, sucursales, etc. Ya no es paranoia lo del principal, sino simplemente reconocer que las realidades son muy distintas y no puede prever todas las contingencias.
Toikka y Dai dicen que un esquema de incentivos alinea los intereses de los agentes si existe una constante k tal que para cualquier par de productos posibles y & y’, lo que cambian los sueldos del individuo 1 entre esos dos productos es una proporción fija de lo que cambian los sueldos de 2:
w1(y) – w1(y’) = k [w2(y) – w2(y’)]
(y lo mismo para los demás agentes). Gráficamente, lo que dice es que si ponemos los sueldos de 1 en un eje y los de 2 en el otro, todas las realizaciones de pagos que pueden recibir los agentes caen sobre un segmento de recta.
Uno de sus teoremas principales dice que si el esquema de sueldos propuesto por el principal no alinea los incentivos de los agentes, entonces el principal recibirá algo muy parecido al peor resultado posible.
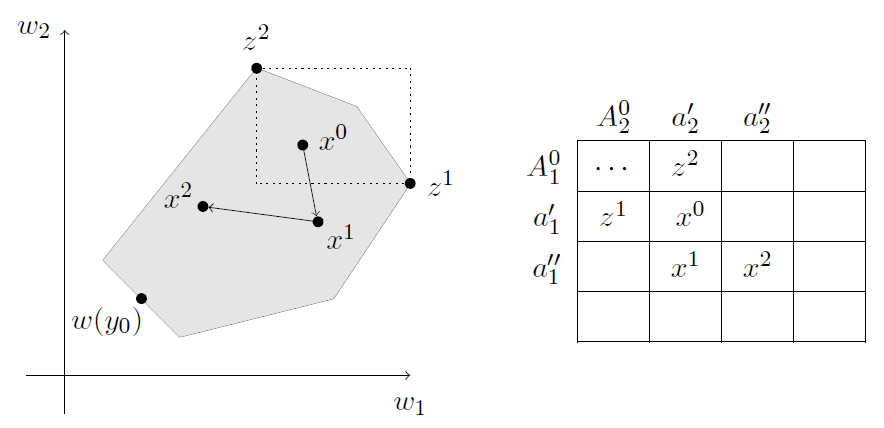
El argumento general para mostrar este resultado es un poco más complicado que el del esquema tipo “bono”, pero no mucho. Si sobrevivieron hasta aquí, va una segunda vuelta de tuerca. En el siguiente gráfico (tomado de la presentación de Toikka), los ejes representan los sueldos que reciben los agentes 1 y 2 en un esquema que no alinea los incentivos; z1 representa el mejor resultado que podría recibir el agente 1, y z2 lo mismo para el agente 2; y w(y0) es el esquema de sueldos correspondiente al peor resultado posible para el principal. En gris están todos los niveles conjuntos de sueldos que pueden recibir los agentes.
El principal sabe que los agentes pueden elegir las Acciones en A0 (en la matriz de la derecha); esas las conoce, no se las imagina. Pero se imagina que los agentes tienen disponibles las acciones a’ (boicotear, sabotear):
- Si 2 no sabotea, la acción a’1 le da a 1 su mejor resultado posible (z1);
- si 2 también boicotea, la acción a’1 le da x0 que es mejor que z2.
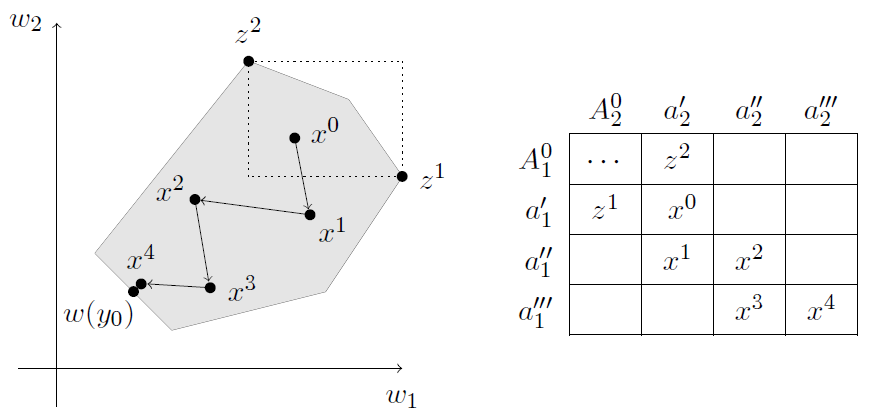
Por lo tanto, cualquiera sea la acción de 2, a’1 domina a cualquier acción de 1 en A0. Lo mismo para 2. Pero x0 no es tan malo como recibir y0 (que es lo que promete el teorema). Lo que pasa es que ahora el principal piensa: ¿y si tuvieran disponibles acciones a’’ que resultaran en los siguientes x?
En este caso, el individuo 1 prefiere jugar a’’1 cuando 2 juega a’2 (le da mayor utilidad), y a su vez 2 prefiere jugar a’’2 contra a’’1. Este proceso se puede continuar hasta estar tan cerca como querramos de y0.
Como x4 está por encima de w(y0), todavía podemos encontrar niveles de utilidad u0<u1<u2<xk para todo k; con esos u rellenamos la tabla de la derecha para que por debajo de todos los x para rellenar la tabla, de tal manera que el juego se puede resolver por eliminación iterada de estrategias dominadas, y ambos juegan a’’’. Por ejemplo, si 2 ya no juega nada en A0, a’1 es dominada por a’’1. Dado eso, a’’2 domina a a’2, etc, etc.
En definitiva, vale la intuición del principio: si no sabemos qué cosas pueden hacer los empleados, lo más razonable es alinear los incentivos, y así se evita la espiral descrita. Es un fundamento teórico elegante para los contratos que observamos en la realidad.
Lo único que no me encanta de todo el asunto, es que para decir “contratos lineales son mejores”, alcanzaría con un argumento más sencillo: con sólo imaginarnos que existen las acciones a’, ya tenemos que podría resultar x0; mostrando que un contrato lineal podría dar algo mejor que el que lleva a x0, ya alcanza para decir que para cada contrato que no alinea resultados, hay uno lineal mejor. No hay necesidad de ir “hasta y0”, que es radical, y sorprendente, y “cute”, pero requiere un principal completamente paranoico.


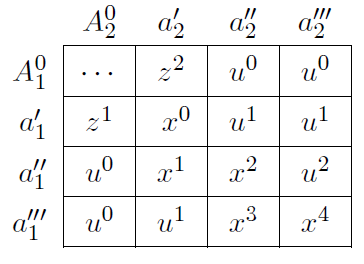



















Buenas, puede recomendarme Papers sobre implementación de incentivos para empleados.
Gracias
Hola César. No sé mucho de la parte práctica de cómo diseñar incentivos para empleados, pero enseño la teoría económica básica sobre cómo debería hacerse. Puedes ver mis notas de clase en el capítulo de «Agente principal» aquí
http://www2.um.edu.uy/dubraj/documentos/notes/teoriainformacion.pdf
o en cualquier libro de micro, en «Moral Hazard». Hay muchos buenos (menciono al Microeconomic Analysis de Varian, pero también es bueno el de Kreps).
Saludos
Juan Dubra