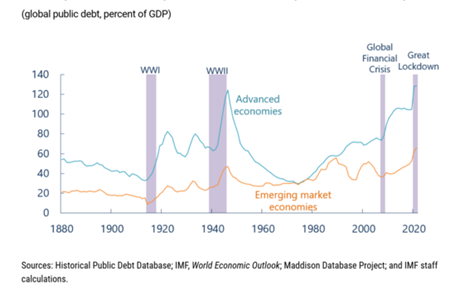
Los niveles de deuda pública globales han alcanzado máximos históricos después de los grandes paquetes de estímulo fiscal que la mayoría de los países han implementado en respuesta a la epidemia de COVID-19 (Gráfico 1). A raíz de esto, se han reavivado las propuestas que plantean la emisión de bonos soberanos atados al PBI como estrategias para reducir la probabilidad de costosas crisis de deuda (FMI 2020). Estos instrumentos de deuda contingentes permiten a los gobiernos reducir sus repagos en tiempos de vacas flacas y en teoría podrían traer muchos beneficios: reducir la probabilidad de default y la ciclicidad de la política fiscal, y además mejorar el reparto de riesgos entre el país y sus acreedores (Hatchondo y Martinez, 2012; Bertinatto et al 2017).
Gráfico 1. World Economic Outlook, Junio 2020
A pesar de estos beneficios, que han sido estudiados extensamente en la literatura, el uso de estos instrumentos ha sido muy escaso en la práctica y los países no han sido capaces de emitirlos a un precio razonable. Tomemos como ejemplo la valuación del bono cupón PBI que emitió Argentina en 2005: se estima una prima de riesgo que rondó entre los 600 y 1200 puntos básicos por sobre la prima de riesgo de default (Costa et al. 2008). Generalmente se ha interpretado que esta prima refleja la “novedad” de los bonos: un extra que los inversores demandan dado que no están familiarizados con estos instrumentos. Sorprendentemente, hay muy pocos estudios teóricos que investiguen las razones subyacentes de dicha prima y la falta de indexación en los mercados de deuda soberana sigue siendo una incógnita.
¿Por qué los bonos vinculados al PBI han cotizado tan desfavorablemente?
En Roch y Roldán (2021), desarrollamos un marco teórico que nos permite racionalizar los bajos precios de estos bonos observados en la realidad. Nuestro modelo incorpora un mecanismo habitualmente utilizado en finanzas para resolver la paradoja de las primas de las acciones (equity premium puzzle) y nos permite entender por qué estos bonos contingentes no han tenido éxito hasta el momento. En resumen, en vez de resaltar lo que los inversores saben que no saben, sugerimos que el obstáculo puede estar más bien relacionado a lo que los inversores no saben que no saben. En particular, analizamos cómo la preocupación por parte de los inversores internacionales sobre errores de especificación de su modelo estadístico (es decir, que el modelo falle en advertirles sobre incógnitas desconocidas) puede afectar los beneficios de emitir bonos vinculados al PBI.
Evaluamos los precios y las implicancias sobre el bienestar de los bonos contingentes usando un modelo estándar de deuda soberana y default, incorporando preferencias por robustez a errores de especificación en el modelo por parte de los inversores internacionales (Hansen y Sargent, 2001; Pouzo y Presno, 2016). Los inversores tienen en mente un modelo estadístico para evaluar los posibles estados de la naturaleza futuros, pero no confían del todo en ese modelo. Por lo tanto, consideran modelos alternativos plausibles y toman decisiones que funcionen bien bajo todos estos modelos alternativos.
Los bonos contingentes que los países han emitido en la práctica generalmente presentan una estructura por la cual solo se prometen repagos cuando el crecimiento del PBI supera un cierto umbral (por ejemplo: Argentina 2005, Grecia 2012, Ucrania 2015). Nuestro marco teórico con acreedores robustos genera una prima por “ambigüedad” que, para esta estructura de umbral, puede explicar la mayor parte de lo que usualmente se lo llama prima por novedad (es decir, el residuo del spread una vez que se quita la prima de default). En la medida que los inversores busquen reglas de decisión robustas que se desempeñen bien bajo todas las contingencias posibles (conocidas y desconocidas), se comportan como si las probabilidades de los estados de la naturaleza “malos” fueran más altas. Para los acreedores, los estados de la naturaleza malos son aquellos en los que no reciben pagos. Por lo tanto, demandan una compensación para tener en su cartera bonos que prometan repagos más variables. Esta fuente adicional de prima genera pérdidas de bienestar para el gobierno emisor.
Un ejemplo simple
Para ilustrar cómo las preferencias por robustez afectan a los precios de los bonos, imaginemos un país que enfrenta la siguiente distribución de probabilidades respecto a su ingreso futuro:
| Crisis | Bajo | Normal | Alto | Boom | |
| Probabilidad | 10% | 20% | 40% | 20% | 10% |
Primero supongamos que el país emite bonos no contingentes que prometen un repago de una unidad independientemente de la realización del ingreso futuro pero que es sabido que habrá default en el estado de Crisis. Los inversores anticipan un repago de 0 con 10% de probabilidad y un repago de 1 con 90% de probabilidad. Sin embargo, los inversores con preferencias por robustez no confían plenamente en dicha distribución y temen que la probabilidad del estado de crisis sea mayor. Por eso, terminan valuando el bono con las siguientes probabilidades distorsionadas
| Crisis | Bajo | Normal | Alto | Boom | |
| Probabilidad | 10% | 20% | 40% | 20% | 10% |
| Pago estipulado | 1 | 1 | 1 | 1 | 1 |
| Default | Sí | No | No | No | No |
| Probabilidades distorsionadas | 23% | 17% | 34% | 17% | 9% |
Los inversores sobreestiman la probabilidad del estado de Crisis en el cual no reciben repagos. Simétricamente, subestiman la probabilidad de los otros estados. Vale la pena notar que en nuestro modelo un bono contingente que establezca un repago de 0 en el estado de Crisis y un repago de 1 en los otros estados (replicando la estructura esperada de repagos del bono no contingente) induciría las mismas distorsiones de probabilidades y, por lo tanto, los mismos precios que un bono no contingente.
Comparemos ahora el bono no contingente con un bono que prometa repagos con un umbral ubicado en los estados favorables. Es decir, el bono estipula repagos de 1 a partir del estado Normal.
| Crisis | Bajo | Normal | Alto | Boom | |
| Probabilidad | 10% | 20% | 40% | 20% | 10% |
| Repago estipulado | 0 | 0 | 1 | 1 | 1 |
| Default | No | No | No | No | No |
| Probabilidades distorsionadas | 18% | 36% | 26% | 13% | 7% |
En este caso, los inversores anticipan un repago de 0 con 30% de probabilidad y de 1 con 70% de probabilidad. Si bien la probabilidad distorsionada del estado Crisis es ahora menor que en el caso anterior, la distorsión adicional que eleva la probabilidad del estado Bajo contribuye a una mayor magnificación del evento de no repago. Dicho de otra manera, la probabilidad distorsionada del estado Normal-o-mejor era del 61% para el caso de deuda no contingente, mientras que es del 46% con la deuda con un umbral más elevado. Estas mayores distorsiones generan una prima por ambigüedad significativa asociada a la estructura de umbral que explica que el gobierno prefiera emitir el bono no contingente.
Los inversores quieren ser robustos a pequeñas desviaciones en su evaluación de probabilidades de diferentes estados de la naturaleza futuros. Un estado poco probable va a continuar siéndolo ante pequeñas distorsiones en el modelo subyacente. Sin embargo, distorsionar probabilidades de los estados más probables tiene efectos más significativos. En el caso de deuda no contingente, la probabilidad del estado de la naturaleza sin repago pasa del 10% sin distorsiones al 23% con distorsiones. En cambio, aumenta del 30 al 54% para el caso de la deuda con umbral.
El diseño importa
Nuestro trabajo sugiere que, si los inversores tienen preferencias por robustez, la estructura de los pagos estipulados en el bono importa. Alterar la estructura de repagos dejando fijo el repago esperado no afecta el precio que inversores con expectativas racionales (el supuesto estándar en la literatura de deuda soberana) ofrecen por el bono. Sin embargo, cuando los inversores son robustos, cambios en la estructura de repagos habilitan distorsiones de probabilidad. Estas distorsiones generan una prima por ambigüedad y contribuyen a spreads más altos.
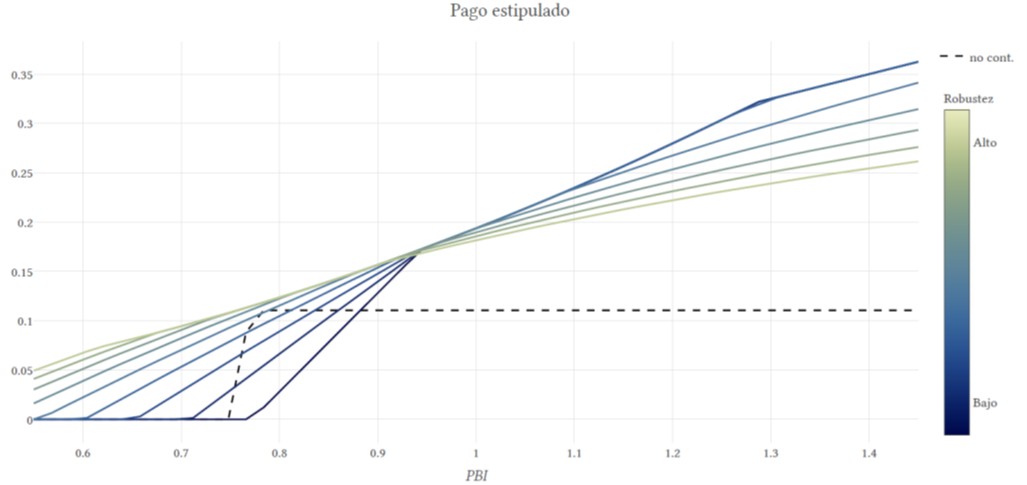
Por lo tanto, el diseño óptimo del bono contingente depende del grado de preferencia por robustez de los inversores. A mayor robustez, la estructura óptima presenta un menor grado de contingencia, menores pendientes en los repagos y regiones más chicas en las que el repago prometido es cero (Gráfico 2). Es decir, diseñar la estructura óptima del bono contingente conlleva una disyuntiva importante cuando el gobierno enfrenta inversores robustos. Por un lado, el gobierno emisor querría minimizar el grado de contingencia en los repagos para limitar las distorsiones de probabilidad y así pagar una prima baja. Pero, por otro lado, también necesita minimizar otra fuente de contingencia que proviene del riesgo de default ex-post. Para los estados malos, el gobierno promete lo máximo que pueda comprometerse a repagar de manera creíble. Esta disyuntiva limita el alcance de reparto de riesgos entre el gobierno y sus acreedores. A diferencia del bono con umbral que los países han emitido en el pasado, el diseño óptimo del bono contingente genera significativas mejoras de bienestar (aunque estas ganancias son menores cuanto más robustos sean los inversores).
Gráfico 2. Diseño óptimo del bono contingente
Conclusiones
La preferencia por robustez por parte de los inversores ayuda a explicar los precios observados de los bonos contingentes. En nuestro trabajo existe una relación directa entre los precios de los bonos contingentes con la estructura que típicamente han exhibido: un umbral que establece repagos solo si el crecimiento económico supera la media. Esta estructura, que estipula repagos de 0 para una gran fracción de las potenciales contingencias, es particularmente susceptible a las distorsiones de probabilidades de los inversores con preferencias por robustez. Nuestro modelo calibrado a los datos de Argentina puede explicar los precios de los bonos cupón PBI emitidos en la reestructuración de 2005. Nuestros hallazgos permiten racionalizar el escaso uso de estos instrumentos en la práctica e informan sobre su diseño óptimo. Estas consideraciones son especialmente relevantes dado el renovado interés en los bonos contingentes por los elevados niveles de deuda soberana y de incertidumbre sobre las perspectivas económicas debido al COVID-19.
Referencias
Bertinatto, L., Gomtsyan, D., Sandleris, G., Sapriza, H., and Taddei, F. (2017). ‘Indexed Sovereign
Debt: An Applied Framework’. Mimeo.
Costa, A., Chamon, M., and Ricci, L. (2008). ‘Is There a Novelty Premium on New Financial Instruments? The Argentine Experience with GDP-Indexed Warrants’. IMF Working Paper 08/109.
Hansen, L. and Sargent, T. J. (2001). ‘Robust Control and Model Uncertainty’. American Economic
Review, volume 91, no. 2, 60–66.
Hatchondo, J. C. and Martinez, L. (2012). ‘On the Benefits of GDP-Indexed Government Debt:
Lessons from a Model of Sovereign Defaults’. Economic Quarterly, volume 98, 139–157. No. 2.
IMF (2020). ‘The Role of State-Contingent Debt Instruments in Sovereign Debt Restructurings’.
Staff discussion notes, International Monetary Fund.
Pouzo, D. and Presno, I. (2016). ‘Sovereign Default Risk and Uncertainty Premia’. American Economic Journal: Macroeconomics, volume 8, no. 3, 230-66.
Roch, F. and Roldán, F. (2021). ‘Uncertainty Premia, Sovereign Default Risk, and State-Contingent Debt‘. IMF Working Paper 2021/076.