En este texto exploramos si la disminuciA?n observada en las cifras de pobreza extrema publicadas el aA�o pasado por CONEVAL pueden ser atribuibles a errores de estimaciA?n del algoritmo de imputaciA?n diseA�ado para que las cifras de ingresos de los hogares de 2016 sean comparables con las de 2014. La respuesta corta es que sA�: encontramos que el algoritmo de imputaciA?n parece sobreestimar de manera importante el cambio en el ingreso de los hogares mA?s pobres del paA�s[1].
En agosto de 2017, el Consejo Nacional De EvaluaciA?n de la PolA�tica Social (CONEVAL) presentA? su informe sobre la evoluciA?n de las cifras de pobreza en MA�xico. En suma, seA�ala que el porcentaje de mexicanos que viven en condiciA?n de pobreza se redujo modestamente (de 46.2% a 43.6%), y que observamos una importantA�sima disminuciA?n (la mA?s alta en la historia reciente de MA�xico) en el porcentaje de la poblaciA?n en condiciones de pobreza extrema, de 9.5% en 2014 a 7.6% en 2016 (A?una disminuciA?n cercana al 20%!). La prensa y el gobierno festejaron la noticia. No obstante, estas cifras fueron calculadas despuA�s de ajustar los ingresos reportados por los hogares en 2016 usando un algoritmo diseA�ado por un grupo de expertos convocado por el INEGI y el CONEVAL para permitir su comparabilidad con encuestas anteriores pues, a partir de 2015, se introdujeron algunos cambios metodolA?gicos que tuvieron un impacto importante en los ingresos reportados por los hogares. En este texto, buscamos inferir la magnitud de los errores de imputaciA?n asociadas al algoritmo de imputaciA?n utilizadoA�[2].A�Para hacerlo, empezamos por describir los datos que dieron origen a la creaciA?n del grupo de expertos que lo diseA�A?.
Empecemos por calcular el cambio en el ingreso por decil de la poblaciA?n entre 2014 y 2016 antes de aplicar el ajuste estadA�stico (Figura 1). Si la informaciA?n contenida en ambas encuestas fuera comparable, la informaciA?n presentada en esta figura serA�a una extraordinaria noticia: entre 2014 y 2016, los hogares mA?s pobres del paA�s observaron incrementos gigantescos en sus ingresos.
Figura 1. Cambio Porcentual en el Ingreso Corriente por Decil de la PoblaciA?n Sin Ajustes (2014-2016)*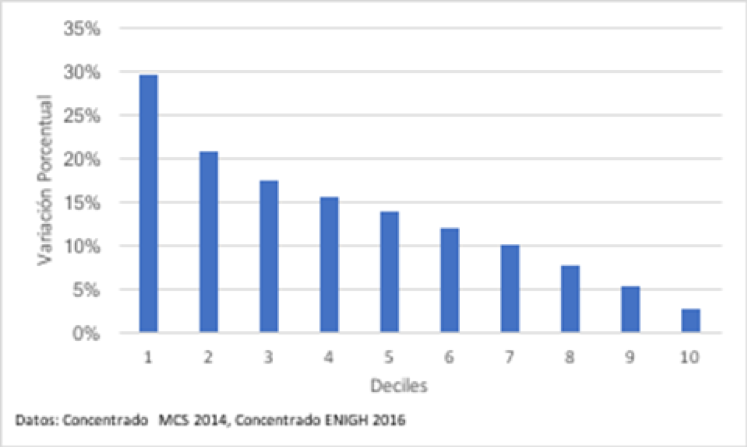
*CA?lculos propios. Excluye el 1% de hogares que reportan los ingresos mA?s altos.
En 2016, sin embargo, organizaciones de la sociedad civil (en particular el CEEY y OXFAM), junto con un amplio grupo de acadA�micos expertos en temas relacionados con la economA�a del desarrollo, hicieron pA?blica su preocupaciA?nA�sobre el hecho de que el INEGI habA�a cambiado la metodologA�a para medir el ingreso de los hogares mexicanos. El llamado de atenciA?n respondA�a a que parecA�a imposible inferir si el aumento en los ingresos de los hogares presentado en la Figura 1 correspondA�a al que habrA�amos observado en ausencia de los cambios metodolA?gicos para el levantamiento de estas encuestas[3].
El llamado de atenciA?n dio resultado y el INEGI, junto con el CONEVAL, reunieron a un a�?Grupo TA�cnico Ampliadoa�? para diseA�ar un algoritmo de imputaciA?n para las encuestas posteriores a 2014 que permitiera la comparabilidad de los ingresos de los hogares en el tiempo. La tarea era dificilA�sima, pues es imposible determinar con exactitud cuA?nto del cambio observado en los ingresos presentados en la Figura 1 se debe al cambio metodolA?gico y cuA?nto efectivamente a un aumento real en los ingresos de las personas. Hoy, sin embargo, el algoritmo diseA�ado por este grupo de expertos es pA?blico y fA?cilmente descargablede la pA?gina de internet del INEGI.
Pero, A?quA� tan bien predice los cambios en la distribuciA?n del ingreso entre 2014 y 2016 dicho algoritmo?
Para responder esta pregunta, vale la pena volver a la Figura 1 y darnos cuenta de que los cambios metodolA?gicos pueden haber tenido dos consecuencias principales. Por un lado, los ingresos promedio reportados por los hogares mexicanos podrA�an haber aumentado. Y, por el otro, estos cambios metodolA?gicos pueden haber tenido un impacto en la formade la funciA?n de distribuciA?n del ingreso reportado. Cualquier procedimiento que busque revertir los cambios en la distribuciA?n del ingreso que resultan del cambio metodolA?gico debe, por lo tanto, hacer un esfuerzo por inferir no sA?lo el promedio o la mediana del ingreso, sino tambiA�n la formaque tomarA�a la funciA?n de distribuciA?n del ingreso en ausencia de estos cambios.
El algoritmo de imputaciA?n diseA�ado por el grupo tA�cnico ampliado no hace esto A?ltimo. En tA�rminos simples, recupera la 20 generic mg nolvadex formaA�de la distribuciA?n del ingreso A?nicamente a partir de la informaciA?n en la encuesta levantada despuA�s de los cambios metodolA?gicos. Y, dada esta forma general de la distribuciA?n del ingreso, ajusta sus parA?metros con el A?nico objetivo de que el cambio en la mediana del ingreso en cada estado reportado en el mismo perA�odo por los hogares en otra encuesta que no sufriA? cambios metodolA?gicos (la ENOE), coincida con el cambio que se observa entre 2014 y los valores del ingreso imputados en 2016.
Para ilustrar de la forma mA?s sencilla posible por quA� el mA�todo elegido por el grupo tA�cnico ampliado puede arrojar resultados equivocados, presentamos un ejercicio simple en el que introducimos una pequeA�A�sima variaciA?n al procedimiento que realizan: en lugar de recuperar la formade la distribuciA?n del ingreso en 2016, recuperamos la forma de la distribuciA?n del logaritmo natural del mismo. Es decir, realizamos una muy simple transformaciA?n a nuestro objeto de interA�s.
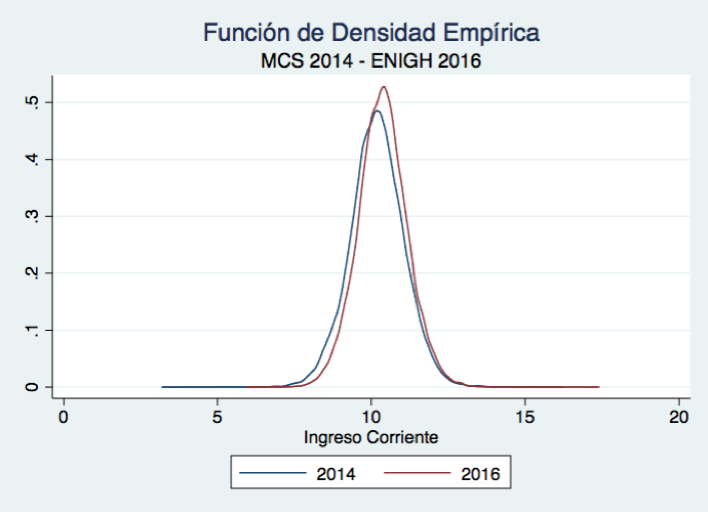
La Figura 2 muestra las funciones de densidad empA�ricas del logaritmo del ingreso de 2014 y 2016 (antes del ajuste estadA�stico).A� Resaltan tres hechos principales: 1) ambas funciones son (mA?s o menos) simA�tricas; 2) la media y mediana del logaritmo del ingreso en 2016 se encuentran mA?s a la derecha que los mismos estadA�sticos para la distribuciA?n del logaritmo del ingreso en 2014; y 3) la distribuciA?n del logaritmo del ingreso de 2016 tiene colas menos pesadas que la de 2014. Un algoritmo de imputaciA?n que replique el ajuste estadA�stico sugerido por el grupo tA�cnico ampliado, pero que en vez de ajustar la distribuciA?n del ingreso en 2016 corrija la distribuciA?n del logaritmo de esta misma variable, sA?lo desplazarA�a (hacia la izquierda) la funciA?n de densidad empA�rica de 2016, de forma que su mediana coincidiera con la mediana objetivo. No modificarA�a en lo absoluto la forma de esta funciA?n.
Figura 2
Es fA?cil inferir que la diferencia principal entre la distribuciA?n del logaritmo del ingreso en 2016 resultado de este ejercicio y la del logaritmo del ingreso en 2014 estarA�a principalmente en la pesadez de sus colas. Y, que si calculA?ramos entonces el cambio en ingresos por deciles de la distribuciA?n, obtendrA�amos un resultado prA?cticamente igual al presentado en la Figura 1. SA?lo habrA�a que restarles a todas las barras exactamente el mismo nA?mero. En otras palabras, los resultados de este ejercicio sugerirA�an un muy importante aumento en el ingreso para los primeros deciles de la distribuciA?n del ingreso, y una importante disminuciA?n en los deciles mA?s altos de la misma.
En la prA?ctica, el ajuste estadA�stico utilizado por el CONEVAL no hace exactamente lo descrito en los pA?rrafos anteriores. Sin embargo, la A?nica diferencia importante entre lo arriba descrito y el algoritmo de imputaciA?n es que, en una primera instancia, estima la distribuciA?n del ingreso de 2016, en lugar de la de su logaritmo. Como la funciA?n de densidad del ingreso no puede tomar valores negativos, el ajuste a sus parA?metros para lograr que su mediana coincida con las medianas objetivo definidas a partir de la ENOE es mucho mA?s sofisticado que un simple desplazamiento hacia la izquierda de la funciA?n de densidad. Sin embargo, sigue siendo cierto que, en se segunda etapa, el algoritmo no utiliza mA?s que la mediana como el estadA�stico a ajustar. Y, por eso, sigue siendo posible que los resultados estimen un aumento importante en el ingreso de los deciles mA?s bajos y una disminuciA?n en el ingreso de los deciles mA?s altos de la distribuciA?n del ingreso sA?lo como consecuencia de haber estimado la forma de la distribuciA?n A?nicamente a partir de los ingresos reportados despuA�s del cambio metodolA?gico.
La Figura 3 repite el ejercicio presentado en la Figura 1 esta vez calculando el cambio en el ingreso por decil de la poblaciA?n entre 2014 y los valores imputados en 2016. De nuevo, si la informaciA?n presentada en la Figura 2 efectivamente midiera el cambio en ingresos por deciles, la noticia serA�a casi tan extraordinaria como la que sugiere la Figura 1. Aunque en menor medida, el ingreso de los deciles mA?s bajos de la distribuciA?n del ingreso aumentA? considerablemente y el ingreso promedio de los deciles mA?s altos disminuyA?. Pero, como describimos en el pA?rrafo anterior, la aparentemente buena noticia puede tambiA�n ser A?nicamente consecuencia de los supuestos implA�citos en el algoritmo de imputaciA?n.
Figura 3. Cambio Porcentual en el Ingreso Corriente por Decil de la PoblaciA?n (ENIGH 2014-ImputaciA?n ENIGH 2016)*
A?CA?mo juzgar entonces si el ajuste estadA�stico efectivamente corrige los cambios en el ingreso que habrA�amos observado para cada decil de la poblaciA?n en ausencia del cambio metodolA?gico?
Para responder a esta pregunta, necesitarA�amos (idealmente) contar con una encuesta alternativa que recupere los ingresos de los hogares en 2014 y 2016 que no haya sufrido los cambios metodolA?gicos introducidos despuA�s de 2014. El grupo tA�cnico ampliado menciona (y utiliza para el cA?lculo de las medianas objetivo) a la ENOE. A�Sin embargo, esta encuesta sA?lo recupera informaciA?n sobre el ingreso laboral de los hogares y, desgraciadamente, mA?s del 25 por ciento de los hogares en la muestra reportan un ingreso laboral igual a cero (tanto en 2014 como en 2016). Es imposible entonces recuperar cifras precisas sobre el cambio en el ingreso de los hogares en los deciles mA?s bajos de la distribuciA?n.
Para inferir entonces cuA?nto de los cambios en el ingreso promedio de cada uno de los deciles de la poblaciA?n pueden atribuirse a errores en el algoritmo de imputaciA?n, en este texto hacemos un supuesto defendible y parcialmente verificable: suponemos que, dentro de cada decil de ingresos, la diferencia entre encuestas en porcentaje del ingreso corriente que representa el gasto monetario de los hogares es constante e igual a la que observamos para el quinto decil de ingresos. AdemA?s, suponemos que el error de imputaciA?n para el quinto decil es cero. Como la ENIGH reporta el gasto monetario de los hogares, y porque aparentemente los cambios metodolA?gicos introducidos despuA�s de 2014 sA?lo tienen un impacto importante en las cifras de ingreso reportadas por los hogares, podemos preguntarnos si los cambios porcentuales observados en el ingreso de cada decil corresponden o no a cambios porcentuales de la misma magnitud en su gasto monetario. En caso de que no coincidan, y si nuestro supuesto se cumple, la diferencia entre estas cifras (con respecto a la que observamos para el quinto decil) puede interpretarse como el cambio porcentual en el ingreso atribuible A?nicamente al algoritmo de imputaciA?n.
La Figura 4 presenta los resultados de este ejercicio. Como es evidente, es muy posible que muchos de los cambios en ingresos entre los deciles mA?s bajos y mA?s altos de la distribuciA?n del ingreso se deban A?nicamente al algoritmo de imputaciA?n.
Figura 4. Cambio Porcentual en el Ingreso Corriente por Decil Atribuible a Errores de ImputaciA?nA�2014-2016 (Primera Diferencia)*
*CA?lculos propios. Excluye el 1% de hogares que reportan los ingresos mA?s altos.
La disminuciA?n en las cifras de pobreza extrema que el CONEVAL publicA? el aA�o pasado pueden entonces deberse en gran medida a los errores de imputaciA?n asociados con el ajuste estadA�stico diseA�ado por el grupo tA�cnico ampliado.
Un A?ltimo ejercicio nos puede ayudar a verificar si nuestro principal supuesto de identificaciA?n se cumple. En concreto, si se cumpliera, el patrA?n observado en la Figura 4 no tendrA�a que sufrir cambios muy importantes si a las cifras reportadas les restA?ramos la misma diferencia (entre el crecimiento del ingreso corriente y el gasto monetario), pero entre aA�os anteriores a 2016, cuando sabemos no hubo cambio metodolA?gico alguno. La Figura 5 presenta los resultados de este ejercicio: Si bien las cifras sufren algunos cambios con respecto a las de la Figura 4, el gradiente general se mantiene: el algoritmo de imputaciA?n parece sobreestimar el ingreso de los hogares mA?s pobres y subestimar el de los mA?s ricos.
Figura 5. Cambio Porcentual en el Ingreso Corriente por Decil Atribuible a Errores de ImputaciA?nA�2014-2016 (Estimador de Dobles Diferencias)
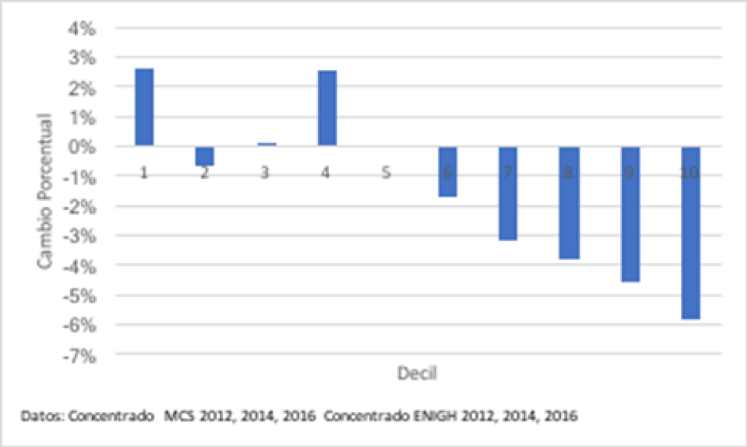*CA?lculos propios. Excluye el 1% de hogares que reportan los ingresos mA?s altos.
Con este ejercicio, no buscamos mermar la confianza que los mexicanos tenemos en el CONEVAL. Como ya mencionamos, recuperar la forma de la distribuciA?n del ingreso de 2016 en ausencia de los cambios metodolA?gicos es una tarea dificilA�sima. Por eso, sabemos tambiA�n que nuestros cA?lculos no son definitivos y estA?n sujetos a crA�ticas. Esperamos, sin embargo, que este texto contribuya al inicio de un debate entre la comunidad cientA�fica donde se propongan y discutan pA?blicamente algoritmos de imputaciA?n alternativos que entiendan la pregunta en cuestiA?n y busquen efectivamente minimizar los errores en la estimaciA?n.
[1]A�Este texto es un resumen del primer capA�tulo del borrador de tesis de licenciatura que A?ngel Espinoza (estudiante del ITAM) estA? escribiendo bajo la asesorA�a de Emilio GutiA�rrez.
[2]Otros autores han ya A�cuestionadoA�el algoritmo de imputaciA?n utilizado para comparar las cifras de pobreza de 2014 y 2016. El ejercicio que presentamos sA?lo es posible dado el compromiso del CONEVAL y el INEGI con la transparencia, pues las bases de datos y programas que utiliza para el cA?lculo de las cifras de pobreza (asA� como el algoritmo de imputaciA?n) son de facilA�simo acceso en su pA?gina de internet.
[3]Los cambios metodolA?gicos introducidos por INEGI en las encuestas posteriores a 2014 son principalmente cambios al entrenamiento de los encuestadores. Los cuestionarios son los mismos, pero se instruyA? a los encuestadores a insistir en las preguntas relacionadas con ingresos para recuperar cifras presuntamente mA?s precisas (sobre todo para los hogares de menores ingresos).
