Medición de la inflación: No violemos la ley (de los grandes números)

Junto a Alberto Cavallo (MIT) y Ricardo Nicolás Pérez-Truglia (Harvard)

Aunque para algunos de eso no se habla, la inflación en Argentina es un tópico recurrente en Foco Económico (qué sabemos sobre ella, cuáles son sus costos – demasiados links para citarlos todos…), y por buenas razones – tanto por la historia económica del país como por la centralidad de este tema para la situación actual de la economía. También se abordó en estas páginas el tema de la intervención del INDEC y de la manipulación del índice de precios al consumidor, dañina e inútil como la denomina Juan Pablo Nicolini en este clarísimo post.

Desafortunadamente, como consecuencia de la opacidad del índice oficial, la proliferación de indicadores alternativos (que como argumentamos más abajo ayuda a obtener un mejor estimador) también es aprovechada para intentar sembrar dudas sobre la validez de estas mediciones. La última serie de este debate se dio en torno a la (tardía) publicación del índice de precios de la Ciudad Autónoma de Buenos Aires, basado en 60000 precios de una canasta de 600 productos relevados en 3200 comercios. Las críticas suelen concentrarse en supuestos sesgos sistemáticos que surgen de la composición y los tamaños de las canastas utilizadas para estas medidas alternativas. El objetivo de este breve post es modesto, y en el fondo no constituye más que una simple aplicación de la ley de los grandes números: queremos ilustrar con un ejemplo muy simple cómo con recursos relativamente modestos podemos obtener buenas medidas de la inflación, como las que de hecho estamos obteniendo.

Es importante empezar aclarando que la medición de la inflación es una disciplina en la que contamos con décadas de experiencia nacional e internacional, expertos sobre el tema, convenciones internacionales y una extensa literatura técnica y académica. No es una tarea sencilla, por lo que siempre el ideal será contar con un instituto de estadísticas con recursos económicos y técnicos que releve y analice precios de manera fidedigna y sistemática.

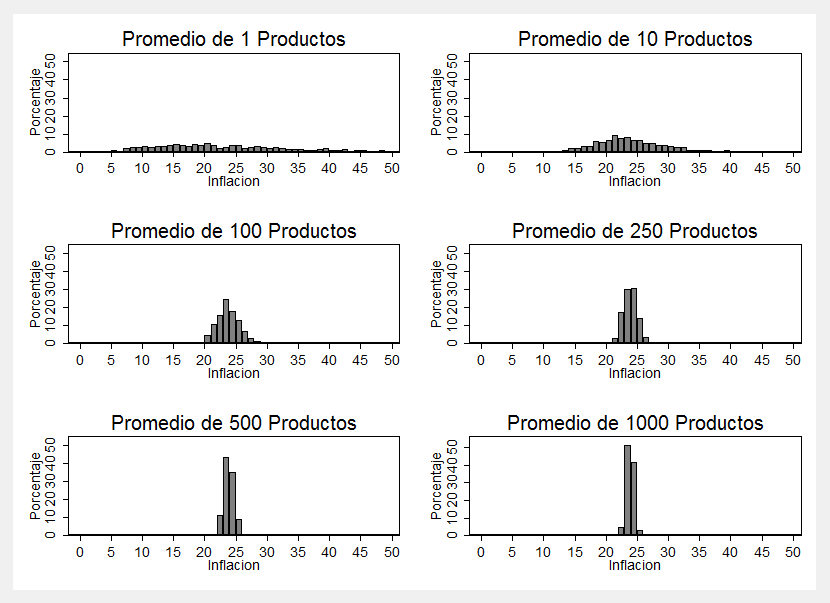
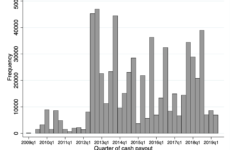
¿Qué podemos hacer cuando no contamos con esto? Sin querer minimizar la importante tarea que realizan los institutos de estadística, las simulaciones que presentamos aquí tienen el objetivo de ilustrar cómo con recursos relativamente modestos podemos obtener buenos resultados para aproximar el aumento generalizado de precios. Tomamos una base de datos recolectada por el Billion Prices Project del MIT con casi 10000 productos de un supermercado en Buenos Aires, y usamos los precios del 1 de Marzo de 2012 y del 1 de Marzo de 2013. El promedio simple de cambios de precios es de 23.95%. En base a estos cambios de precios, computamos 1000 “índices” de inflación para canastas de J bienes seleccionados al azar (sin reposición), con J=1, 10, 100, 250, 500 y 1000. El gráfico a continuación muestra la distribución de los 1000 índices computados para cada tamaño de canasta (J):

La “canasta” de 1 producto (J=1) ilustra el amplio rango de variación en los cambios de precios individuales (recortados en 0 y 50% para el gráfico): claramente, no podemos usar un solo precio como indicador de inflación, porque si bien los precios suben en promedio en 24% hay una amplia variedad de subas y bajas. La distribución de índices con canastas de 10 productos (J=10) es notablemente más concentrada, pero aún tiene una gran dispersión.

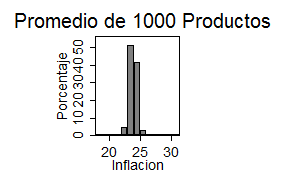
La “concentración” de los indicadores se incrementa con el tamaño de la canasta. Con 1000 canastas de 1000 productos, el 90% de los índices cae entre 23% y 25%:

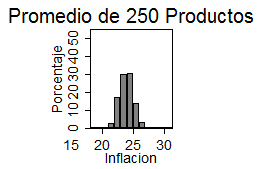
Estas canastas ficticias fueron seleccionadas al azar y no responden a ningún criterio. Mientras tengamos buenos datos, sin ningún sesgo importante, tendremos problemas de precisión pero le vamos a “pegar”, en promedio, a la media – y de ahí la importancia de la agregación de índices. Lo notable es que con canastas de 250 productos, que podemos pensar que representa un esfuerzo razonable para una institución como una universidad o un sindicato, ya tenemos estimadores que podemos considerar relativamente buenos:

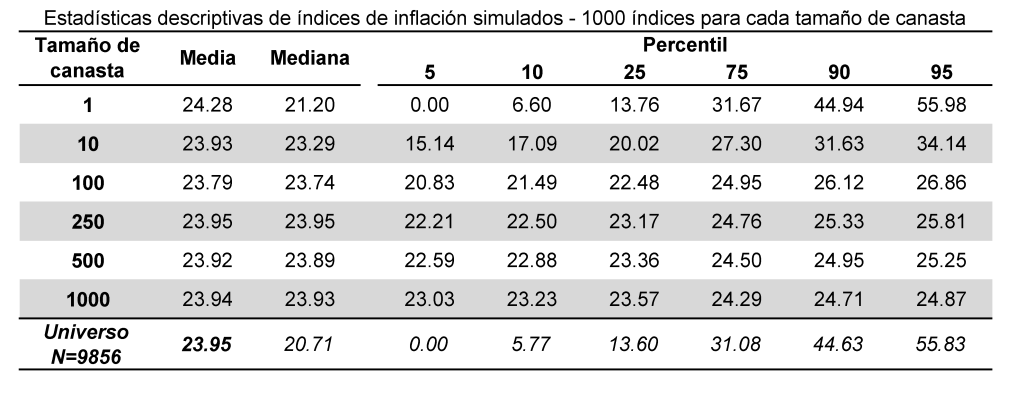
Como puede verse en la tabla de más abajo, con 1000 índices basados en canastas de 250 productos, el 90% de esos índices estarán entre 22,5% y 25,81%. Quizás ese rango no tiene una precisión suficiente para realizar una sintonía fina de la política económica, pero sí es suficiente para negociar una paritaria o tomar decisiones en una empresa.

Economistas de diversas orientaciones están manejando índices independientes: por ejemplo, índices oficiales provinciales (el IPC del INDEC corresponde al GBA), y estadísticas computadas con datos propios, cosa que muchos sindicatos, ONGs, centros de estudios, universidades y consultoras de todos los colores empezaron a hacer a partir de la intervención del INDEC. Algunos optan por la agregación de estas diversas fuentes de datos, como el denominado “IPC-Congreso”, que promedia diversos índices privados y provinciales. En términos de la ley de grandes números, esto es altamente recomendable. Este error de muestreo tiene que ver con observar sub-muestras de productos y se atenuará cuando promediemos distintos estimadores. Además del este error de muestreo, hay una fuente de error que va mas allá del tamaño muestral. Por ejemplo, los datos pueden ser relevados de un número chico de puntos de venta (Luciano Cohan ilustró en parte este punto con un ejercicio hipotético basado en precios ficticios), pueden incluir canastas diferentes (solo bienes, como en nuestro caso, en lugar de bienes y servicios), o quizás son relevados en una región poco representativa. Además de la atenuación del error de muestreo, al promediar varios estimadores minimizamos el tamaño esperado de estas otras fuentes de error.

La publicación del índice de la Ciudad de Buenos Aires, entonces, es una buena noticia: se pone al día con lo que realizaban otros distritos sub-nacionales, y nos dan un número más para promediar en la canasta de índices. Con los recursos y la expertise de estadísticas de un distrito grande, contamos con un buen ersatz del antiguo IPC del INDEC, basado en el GBA. Como dice Nicolini, “si dos oficinas igualmente serias y competentes, midieran la tasa de inflación en la ciudad de Buenos Aires, no obtendrían el mismo número – pero sí podrían darnos el margen de error estadístico.” El gobierno de la Ciudad no debería conformarse con poco: podría responder e incorporar las críticas constructivas que se le realizaron, publicar series más largas, y tener su propia página (y no solo unos PDFs). De hecho, nuestra investigación sobre expectativas de inflación (Cavallo et al., 2013) sugiere que tanto el gobierno de la Ciudad como otras organizaciones que computan sus propios índices deberían ir un paso más adelante en comunicar las estadísticas de inflación. En lugar de limitarse a publicar la cifra de inflación agregada, podrían publicarse los microdatos para uso de los investigadores. Pero sobre todo, deberían tener formas intuitivas de comunicación para que los consumidores de la información puedan entender aspectos como la precisión y la representatividad de los índices, y así confiar en los datos ofrecidos – ver por ejemplo los notables esfuerzos en la materia del Banco Central Europeo, con juego y todo. Podría también implementarse una interfaz interactiva que permita a cada uno armar su propia canasta de productos, como hace el instituto estadístico de Francia.

De hecho, como uno de nosotros mostró, pueden utilizarse herramientas para obtener variaciones diarias de precios, a diferencia de los índices oficiales que son mensuales y tienens rezagos en su publicación (Cavallo, 2012). Por supuesto, no existen índices perfectos, pero esto no significa que sean todos discutibles del mismo modo. Con criterios técnicos y metodológicos serios se puede obtener una buena aproximación a la inflación real.

Referencias

Cavallo, A., Cruces, G. y Pérez-Truglia, R. (2013), Why are inflation expectations so dispersed?, mimeo.

Cavallo (2012) “Online and Official Price Indexes: Measuring Argentina’s Inflation”, Journal of Monetary Economics. Volume 60, Issue 1.