Por Juan R. Hernández, CIDE- juan.hernandez@cide.edu
La paridad de tasas de interés cubierta (CIP, por sus siglas en inglés) es una piedra angular de las finanzas internacionales. Es un indicador de la eficiencia del mercado cambiario y se utiliza, por ejemplo, para fijar el precio de los contratos forward para el intercambio de monedas, informando así sobre las condiciones de liquidez que prevalecen en el mercado de divisas.
La CIP es una condición de no-arbitraje. En principio, cuando esta no se cumple, los inversionistas podrían realizar una serie de transacciones en las que obtendrían una ganancia, sin incurrir en riesgos. Por supuesto, ello se contrapone a que no es posible eliminar el riesgo en las transacciones financieras y obtener una ganancia. De esta forma, se esperaría que las desviaciones de la CIP se disipen rápidamente, es decir, la CIP fluctúa dentro de una “banda neutral”.
La banda captura todos los costos de transacción y el riesgo asociados con arbitraje, esto es, las desviaciones están limitadas por un intervalo donde estas no se consideran como oportunidades de arbitraje.
Considere el lector el siguiente ejemplo para ilustrar el mecanismo que previene el arbitraje. Ante una desviación de la CIP entre el dólar de Estados Unidos (USD) y la libra esterlina (GBP), un inversionista en Nueva York pide prestados 100 USD a cierta tasa de interés. Inmediatamente cambia estos USD a GBP y los presta en el Reino Unido a una tasa de interés fija. Simultáneamente, firma un contrato forward para comprar USD al término del préstamo.
La combinación de tasas de interés en Estados Unidos y Reino Unido, junto con la diferencia entre el precio de la GBP en el mercado “spot” con respecto al precio en el mercado “forward” (prima “forward”), permiten que al final del plazo de los préstamos el inversionista tenga en su poder dinero suficiente para pagar el préstamo inicial con intereses y una ganancia. Otros inversionistas harán lo mismo, y el resultado final es que los precios de los activos se ajustan, eliminando esta oportunidad de arbitraje.
En efecto, desde que Keynes (1923) definió la CIP, se han publicado un número importante de investigaciones que confirmaron su validez, para distintos periodos en el tiempo, y con una creciente sofisticación tanto en los métodos econométricos como en la calidad y frecuencia de los datos.[1]
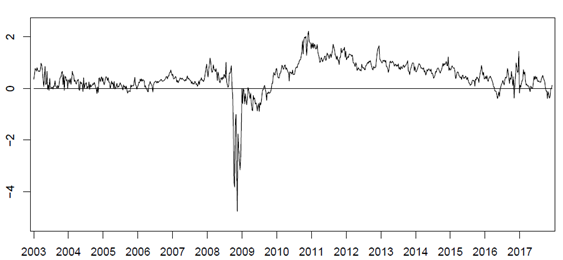
Al respecto, los acontecimientos relacionados con la Crisis Financiera Global (CFG) parecen haber tenido efectos duraderos sobre la CIP, dado que se han presentado desviaciones significativas en los mercados de divisas para las “monedas de reserva” y de mercados emergentes respecto al dólar estadounidense, y dichas desviaciones han sido la norma más que la excepción (Figura 1).
| Figura 1 |
| Desviaciones de la CIP en puntos porcentuales MXN-USD. Calculados con tasa de interés interbancarias a 3 meses. Muestra: enero 7 de 2003 a diciembre 26 de 2017. Cálculos propios para datos semanales. Fuente: Banco de México y Bloomberg. Corresponde con la Figura 3 en Hernandez (2020). |
Como sugiere Levich (2017), las desviaciones de la CIP han motivado una literatura creciente para contestar preguntas como: ¿Qué ocurrió con la CIP? ¿Qué hay detrás de las grandes desviaciones que se han observado? ¿Qué implicaciones hay para los activos financieros que cuyo precio depende de la CIP? Las respuestas que se han propuesto se pueden consultar en la extensa revisión de la literatura que hacen Du y Schreger (2021).
Levich también hizo la siguiente pregunta: Las desviaciones de la CIP que se observan, ¿están contenidas en una “banda neutral” que refleja los costos de transacción y los riesgos inherentes al arbitraje? En Hernandez (2020) se propone una metodología para evaluar si las desviaciones de la CIP están contenidas dentro de la banda neutral.
Con este propósito, se propone una estimación de la amplitud de la banda neutral para tres mercados de divisas durante el periodo 2003-2017: dos mercados que relacionan divisas de “reserva” con el dólar estadounidense, la libra esterlina (USD-GBP) y el euro (USD-EUR); así como el mercado de una economía emergente, esto es, el dólar estadounidense respecto al peso mexicano (USD-MXN).
La contribución de este trabajo consiste en determinar si la mayoría de las desviaciones observadas con respecto a la CIP son replicables por un modelo en el que el arbitraje está ausente. Esto contrasta con la literatura previa de la banda neutral que ha buscado probar si las deviaciones de la CIP están dentro de los límites (constantes) superior e inferior de la banda neutral.[2] En particular, el artículo propone una estimación de la banda neutral basada en un pronóstico de densidad “un paso adelante”, obtenido a partir de modelos de volatilidad estocástica.
Para determinar si las desviaciones con respecto a la CIP pueden ser replicadas por un modelo que supone no-arbitraje, se evalúa la bondad de ajuste al estimar la distribución predictiva de los datos. Al respecto, la banda neutral viene dada por cuantiles del pronóstico de densidad “un paso adelante” para las desviaciones de la CIP. Estos límites pueden variar en el tiempo, lo que permite racionalizar que las restricciones sobre el arbitraje se actualicen con frecuencia en respuesta a la evolución de los mercados financieros.
La estimación se realiza utilizando una muestra en ventanas expansivas. Lo anterior, con el objetivo de replicar la forma en que los participantes del mercado evalúan los costos de transacción y los riesgos que cambian permanentemente en el tiempo y, con ello, tener en una estimación en tiempo real de los límites superior e inferior de la banda neutral.
Los resultados sugieren que los modelos de volatilidad estocástica producen estimaciones superiores de la banda neutral en los tres cruces. Algunas características sugieren que estas estimaciones tienen mejores propiedades que los modelos alternativos. En primer lugar, tienen un mejor desempeño para modelar los datos observados y para pronosticar (i.e. dentro y fuera de muestra). En segundo lugar, son capaces de estimar una banda neutral más amplia en periodos de estrés financiero, lo cual es congruente con los posibles aumentos en los costos de transacción, la aversión al riesgo y la incertidumbre que están asociados a estos periodos. Al respecto, mientras que el modelo utilizado previamente en la literatura estima valores similares para el periodo 2007-2017, el modelo de volatilidad estocástica estima una banda neutral más amplia durante la CFG (Tabla 1).
| Modelo/Periodo | Previo a la CFG
(Dic04-Jun07) |
Durante la CFG
(Jun07-Dec09) |
Post CFG
(Ene10-Dic17) |
| Volatilidad Estocástica* | 28-96 | 28-711 | 36-370 |
| Autorregresivo con umbrales** | 63-83 | 60-145 | 103-137 |
| Tabla 1 | |||
| Rango estimado para la amplitud de la Banda Neutral en puntos base.
La tabla corresponde con la Tabla 3 en Hernandez (2020). |
|||
| *Volatilidad Estocástica corresponde al modelo SV-APF en el artículo. | |||
| **Autorregresivo con Umbrales es el modelo que se ha utilizado previamente en la literatura. | |||
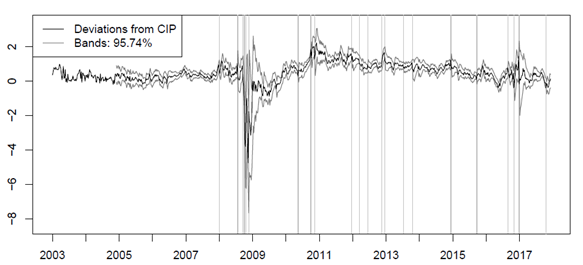
Por último, la estimación de la banda neutral implica que las oportunidades de arbitraje están dispersas en el tiempo y, por lo tanto, son de corta duración, lo cual es consistente con la teoría de precios de activos por arbitraje. En contraste, el modelo de referencia sugiere que las oportunidades de arbitraje están agrupadas en periodos de tiempo y, por tanto, estas son de larga duración o persistentes, lo cual representa una característica difícil de reconciliar con la realidad (Figura 2).
| Figura 2 |
| Desviaciones de la CIP y estimación de la banda neutral en puntos porcentuales MXN-USD. Las líneas verticales señalan los casos en los que las desviaciones de la CIP están fuera de la banda neutral. La etiqueta contiene el porcentaje de observaciones dentro de la banda. Estimaciones propias con datos de Banco de México y Bloomberg. Corresponde con la Figura 6 en Hernandez (2020). |
Finalmente, una de las conclusiones que se derivan de este trabajo, es que la amplitud y la persistencia a través del tiempo de las estimaciones de la banda neutral a través de la volatilidad estocástica es superior ya que puede variar en el tiempo permite reconocer periodos de estrés financiero.
Cabe hacer algunas consideraciones antes de concluir. En primer término, las desviaciones de la CIP parecen estar determinadas por cambios en la regulación financiera que tuvieron lugar a partir de la CFG. Ello implica que, en contraste con la literatura, los cambios abruptos en la CIP contienen más información sobre eventos de estrés financiero. En segundo lugar y asociado al mencionado cambio en regulación, los costos de transacción parecen haberse elevado permanentemente. En particular, ahora se requiere una desviación de la CIP considerable para que los inversionistas tomen las ganancias por arbitraje.
Finalmente, esta literatura tiene diversas avenidas para explorar como sugieren Du y Schreger. Es interesante que una de las relaciones de equilibrio más estables que se podían encontrar en las finanzas internacionales, presente un cambio en su comportamiento notable. Ello, sin embargo, no limita su capacidad para informar sobre las condiciones de liquidez, el proceso de formación de precios de los activos, y las implicaciones de política.
Referencias
- Baba, N. and Packer, F. (2009). Interpreting deviations from covered interest parity during the financial market turmoil of 2007-08. Journal of Banking & Finance, 33(11):1953 – 1962.
- Branson, W. H. (1969). The minimum covered interest differential needed for international arbitrage activity. Journal of Political Economy, 77(6):1028-1035.
- Clinton, K. (1988). Transactions costs and covered interest arbitrage: theory and evidence. Journal of Political Economy, 96(2):358-370.
- Du, W. and Schreger, J. Forthcoming. CIP Deviations, the Dollar, and Frictions in International Capital Markets. Handbook in International Economics. Vol 5, May 2021.
- Einzig, P. (1967). A dynamic theory of forward exchange. Macmillan.
- Frenkel, J. A. (1973). Elasticities and the interest parity theory. Journal of Political Economy, 81(3):741-747.
- Frenkel, J. A. and Levich, R. M. (1975). Covered interest arbitrage: Unexploited profits?. Journal of Political Economy, 83(2):325 – 338.
- (1977). Transaction costs and interest arbitrage: Tranquil versus turbulent periods. Journal of Political Economy, 85(6):1209 – 1226.
- Hernandez, J.R. (2020). Covered Interest Parity: A Stochastic Volatility Approach to Estimate the Neutral Band. Documento de Investigación del Banco de México N° 2020-02.
- Juhl, T., Miles, W., y Weidenmier, M. D. (2006). Covered interest arbitrage: then versus now. Economica, 73(290):341-352.
- Keynes, J. M. (1923). A Tract on Monetary Reform. Macmillan.
- Levich, R. M. (2017). Cip: Then and now, a brief survey of measuring and exploiting deviations from covered interest parity. Remarks prepared for the BIS Symposium: CIP – RIP?
- Peel, D. A. and Taylor, M. P. (2002). Covered interest rate arbitrage in the interwar period and the keynes-einzig conjecture. Journal of Money, Credit & Banking, 34(1):51 – 75.
- Taylor, M. P. (1987). Covered interest parity: A high-frequency, high-quality data study. Economica, 54(216):429-438.
[1] Entre los pioneros en este ámbito están: Einzig (1967); Branson (1969); Frenkel (1973); Frenkel y Levich (1975,1977). Para los años 80, están Clinton (1988); Taylor (1987). Para los años 90 y 2000 Baba y Packer (2009); Peel y Taylor (2002).
[2] La literatura había estimado la banda neutral con dos enfoques. Con un método de “conteo”, en el que la banda se definía como el nivel de la desviación de la CIP que no contenía el 5% de las observaciones (véase Frenkel y Levich, 1975, 1977; Taylor, 1987; Clinton 1988). En contraste, también se ha estimado la banda con técnicas econométricas (véase Branson, 1969; Peel y Taylor, 2002; Juhl et. al. 2006).